댓글을 남기실 수 있습니다.
최석정(崔錫鼎, 1646~1715)은 조선후기 숙종대에 지금의 국무총리 격인 영의정만 8번 역임한 정치인이었다. 그의 정치노선은 현실가능한 정책을 제시하고, 다른 생각을 가진 사람들과 타협하고 소통하는 것이었다. 학문 분야에서도 성리학에 매몰되지 않고 양명학과 서학등 다양한 학문에 관심을 가진 실용주의자였다.
그는 유학 이외에도 수학, 음운학에 이르기까지 다양한 학문에 관심을 가진 학자였다. 특히 수학분야에서 서양 수학을 동양철학에 접목시키려고 했다. 요즘 용어로 치면 융합형 인재였고, 소통형 정치인이었다.
최석정은 숙종대 10번 이상 정승의 위치에 있었던 최고의 정치인이었지만, 오늘날 그 이름이 별로 알려지지 않았다. 그것은 그는 소론의 영수로, 그가 죽은 후 노론을 중심으로 정국이 운영되면서 집권세력이 의도적으로 그의 치적을 과소평가했기 때문으로 보인다.
최석정은 1646년 명문가 집안에서 1646년 태어났다. 그의 할아버지는 병자호란때 주화론(主和論)을 주장하고 영의정까지 역임한 최명길(崔鳴吉, 1586~1647)이었다. 어렸을 때부터 총명했던 그는 17세에 초시 장원을 하고 1671년에 급제하면서 관직 생활을 시작했다. 우의정, 좌의정, 영의정을 모두 지냈으며 영의정만 8번을 포함해 정승만 10번 이상 지냈다. 금수저 출신으로 엘리트 정치인, 관료의 삶을 살았다고 할 수 있다.
1697년 최석정은 이조판서를 거쳐 우의정에 올랐는데 당시 최대 현안은 청나라로부터 세자 책봉을 받는 것이었다. 청나라에서는 대명회전을 근거로 세자 책봉에 미온적인 입장을 보였다.
이에 최석정은 대명회전이 중국의 예식을 정한 것이며, 조선은 외번(外藩)으로 법 적용에 있어서의 차이를 두어야 한다고 주장했다. 그의 주장이 청나라에 받아들여져 세자 책봉이 실현됐다.
그후 승승장구해 좌의정으로 대제학을 겸했고, 1701년 영의정이 되었다. 영의정 때 그는 장희빈의 사사(賜死)를 반대하다가 충청도 진천으로 유배되었다. 유배에서 풀리고 다시 영의정이 되었고, 모두 8번에 걸쳐 영의정을 역임하면서 숙종대 정국을 이끌었다.
숙종의 절대 신임을 받은 최석정은 국가 주요 현안에 손길을 미쳤다. 단종에 대한 복권과 추숭 작업도 그에 의해 완성되었다.
최석정은 사색당파중 소론의 영수였다. 노론과 소론, 남인이 치열하게 대립하는 당쟁의 시대를 살면서 그는 온건하고 합리적인 정치 노선을 추구함으로써 주요 현안을 풀어나갔다.
숙종대 조선사회는 왜란·호란의 후유증이 어느 정도 치유된 상황에서 예론과 북벌론, 등의 정책을 둘러싸고 서인과 남인간의 정책 대립이 격화한 시기였다. 특히 당시 가장 쟁점이 되었던 군제(軍制) 개편과 관련해, 최석정은 양역의 폐단으로 이웃이나 친족이 군역을 지게 되는 백골징포(白骨徵布)와 인징, 족징의 폐단을 언급하고 이의 혁파를 주장했다.
최석정은 현실 가능한 정책부터 점진적으로 해결해 가면서 사회의 모순을 해결해 나가는데 중점을 두었다.
그는 수학에 특히 관심이 많았고, 수학을 증진시키는데 많은 노력을 했다. 그는 박율이라는 수학자가 쓴 산학원본(算學原本)이 발행될 때 서문을 쓰기도 했다.
1686년 중국에 가서 서양의 앞선 학문을 접한 최석정은 <천학초함>(天學初函), <동문산지>(同文算指) 등 중국의 앞선 서적을 가져와 조선에 소개했다.
최석정은 서양학문(西學)의 영향을 받고 공부도 했지만, 이를 동양철학을 바탕으로 정리하려고 했다. 그가 주역철학과 성리학, 양명학에 충분히 이해했기 때문에 가능한 일이었다.
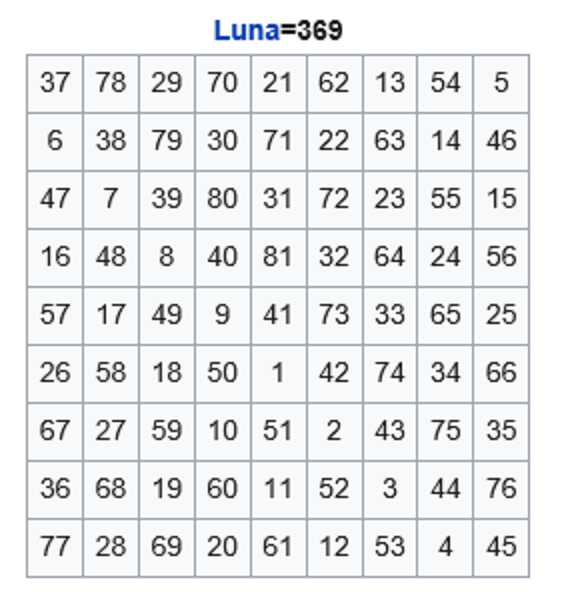
그의 수리철학이 잘 드러나 있는 것이 저작 <구수략>(九數略)이다. 이 책은 동양 고전역학을 바탕으로 당시 수학이론을 정리한 조선시대 대표적 수학서다. 오늘날의 4칙 연산을 각각 태양, 태음, 소양, 소음으로 구분했다. <구수략>은 주역의 괘에 나타난 형상과 변화를 응용해 수리(數理)에 대한 이해를 하고자 하는 상수학적(象數學的)인 인식을 바탕으로 한 책으로 당시의 수학 수준을 보여주고 있다.
<구수략>에는 9차 직교라틴방진(Orthogonal Latin Square)이 게재됐다. 마방진(魔方陣, magic square)이란 이름으로 알려진 9차 직교라틴방진은 가로 세로 9칸씩 81개의 칸에 숫자가 1에서 81까지 하나씩 들어가는 방진이다. 가로, 세로, 대각선 어느 방향으로 더해도 합이 같다. 스위스 수학자 오일러(Leonhard Euler, 1707~1783)가 최초로 발표한 것으로 알려졌으나, 연세대 송홍엽 교수의 노력으로 최석정이 67년 앞섰음이 인정됐다.
수학을 좋아했던 최석정은 자연스럽게 천문역법에도 많은 관심을 보였다. 당시 조선은 청에서 들여온 시헌력(時憲曆)을 사용하고 있었는데 이를 조선 상황에 맞게 해석하는 등 수학을 활용할 일이 많았다.
최석정은 <천학초함>(天學初函)과 같은 외국의 자료를 바탕으로 시헌력과 관련된 천문학을 공부했으며, 1687년에는 ‘선기옥형’(璇璣玉衡)이라는 시계의 수리를 건의하기도 했다. 또한 기상관측 관서인 서운관의 최고 책임자인 서운관영사 역할을 수행하며 천문학 연구에 힘썼다.
최석정은 2013년 한국과학기술한림원에서 제정하는 과학기술인 명예의 전당에 선정됐다.

그래도 삭제하시겠습니까?
댓글을 남기실 수 있습니다.
